为了掌握各类空压机振动的规律,首先要把实际的空压机系统简 化成为它的动力学模型。

例如安装有电动机的梁，它就可简 化成等效的质量一弹簧系统。

梁的弹性，m 相当于电动机的质量。

振动模型可以不止一 个，它主要取决于要求问题的性质和精度等。

一般把振动系 统分成离散参数的和分布参数的两种类型，前者可用有限个 独立参数来确定其位置，后者则不能忽略弹性件的质量，系 统具有连续分布的参数。

对离散振动系统作力分析,可知一般 存在三个作用力，即弹性力、阻尼力、惯性力，它们分别与 以此参数构成成运动微分方程位移、速度和加速度相联系， 式即可研究各类振动的振动特点。

1.单自由度无阻尼线性系统的自由振动

质量系统为单自由度振动系统的最 简单的力学模型。

在无外来激励时，质量m处于平衡位置，弹簧静变 形产生的弹力F= KAs等于质量m承受的重即 力 p= mg,kha= mg(2-25)弹性系数k: 式中弹賃静变形hpt:振动体质量重力加速度。

对振体m给以初始扰动(激励) 振动物体将会在平衡位 置附近发生振动(响应)。

这种系统受初始激励后，振动物体 仅在恢复力(即弹性力)作用下产生的振动,称为自由振动。

按达朗贝尔原理,可列出单自由度线性系统自由振动的 运动方程式:

2.单自由度有阻尼线性系统的自由报动

实际的结构在振动时,会受到种种阻尼力的作用。如材 料内部由于料质不均而发生的微塑性变形产生的阻力，或由 于存在大量细小的裂缝而产生摩擦力，以及外部空气阻力， 元件接点的摩擦等等。

这些阻尼力都要消耗振动能量,使振 其简单也是最常碰到的是粘性阻尼力，其大小和振动衰减, 动速度成正比,即自由振动在计入阻尼作用后产生的振动称为有阻尼的自 由振动。

这时,振动也是非周期性的。

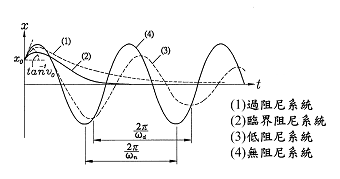
过阻尼和临界阻情况下，动力系统都不会发生振动。在 不同的初始值下,它们的运动情况如图所示。

当初始扰动很小时,系统逐渐趋于平衡; 在特殊初始条 件时,如反向初速度很大,系统最多能有一次移 到平衡位置的另一边。

欠阻尼自由振动具有不变频率ca和相位角9,但振幅按 Ae衰减。

其典型响应曲线，为其 包络线,振幅随时间增长按指数规律递减，逐渐趋向于零。

大多数测振仪器和结构都在欠阻尼条件下工作，为掌握 其振动特点,最主要的要知道阻尼大小，它可通过振幅衰减 系数计算出来

所谓振幅衰减系数，就是衰减振动的波形中 相隔半周的二个振幅绝对值之比。